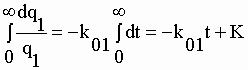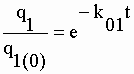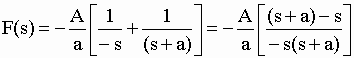Chapitre I Eléments de mathématiques, calcul matriciel, transformations de Laplace |
|||||||||||||
| IV. Transformation de Laplace : une aide à l'intégration des équations différentielles linéaires. | |||||||||||||
| L'intégration "d'équations différentielles linéaires de premier ordre" est l'un des problèmes quelque peu compliqués que nous aurons à résoudre. Ces équations différentielles se présentent souvent en réseaux tels que : | |||||||||||||
| dq1/dt
= - a.q1 +
b.q2 dq2/dt = + c.q1 - d.q2 |
I-60 | ||||||||||||
| où
"q1 et q2" sont des
fonctions exponentielles de la variable indépendante
"t" le temps ; "a, b, c et d" sont
des constantes. Il est facile d’intégrer une équation différentielle linéaire à une seule fonction q1 exprimant par exemple la décroissance physique d'un élément radioactif : |
|||||||||||||
| dq1/dt
= -k01q1 dq1/q1 = -k01dt
lnq1 = -k01t + lnq1(0) |
I-61 | ||||||||||||
| où "ln q1(0)" est assimilé à la constante d'intégration "K" ; q1(0) est la fonction q1 pour t = 0, c'est-à-dire la quantité de radioactivité initiale. | |||||||||||||
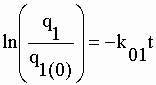
q1 = q1(0)e-k01t |
I-62 | ||||||||||||
| L’intégration
des équations différentielles linéaires décrivant les
systèmes à plusieurs compartiments que nous aurons à
étudier est plus délicate. L’une des méthodes les
plus sures et les plus efficaces utilise la
"transformation de Laplace", mathématicien
français ayant vécu à la fin du 18ème
siècle et au début du 19ème. Elle consiste
à substituer une équation linéaire à une équation
exponentielle. Trivialement elle est aux exponentielles
ce que le logarithme est aux produits. En bref, la
variable indépendante ou temps "t" est
associée à une variable complexe "s" (s = x +
iy où i = |
|||||||||||||
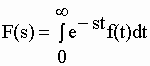 |
I-63 | ||||||||||||
| où
F(s) est la transformée de Laplace de la fonction
exponentielle f(t). F(s) s’écrit aussi Lf(t).
Une fois obtenues les équations des transformées de
Laplace, une nouvelle transformation permet
d’établir les fonctions f(t) classiques
utilisables. On peut démontrer que : a) la transformée de Laplace d’un terme différentiel df(t)/dt est : |
|||||||||||||
| L[df(t)/dt] = sF(s) - f(0) | I-64 | ||||||||||||
| où f(0) est la valeur de f(t) au temps t = 0. Posons u = f(t) et du = [df(t) / dt], dv = e-s.t et v = e-s.t / -s, de même que la primitive de emx est emx / m la primitive de dv = e-st est v = e-st / -s. La formule classique de la primitive d’un produit de deux fonctions : | |||||||||||||
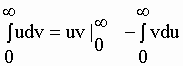 |
I-65 | ||||||||||||
| nous permet d’écrire que : | |||||||||||||
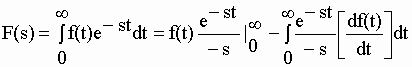 |
|||||||||||||
| puisque
e-st=1 à t = 0 et 0 à t = |
|||||||||||||
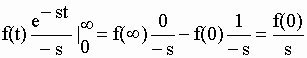 |
|||||||||||||
| il s’ensuit que : | |||||||||||||
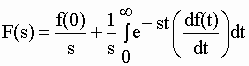 |
|||||||||||||
| et que : | |||||||||||||
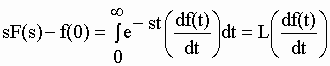 C.Q.F.D. C.Q.F.D. |
I-66 | ||||||||||||
| b) La transformée de Laplace est linéaire : | |||||||||||||
| L[f1(t) + f2(t)] = Lf1(t) + Lf2(t) | I-67 | ||||||||||||
| De même | |||||||||||||
| L[C.f(t)] = C.Lf(t) = C.F(s) | I-68 | ||||||||||||
| où
C est une constante. Par la suite pour simplifier nous
écrirons Findice au lieu de F(s),
l’indice étant un numéro de fonction. Considérons l'équation : |
|||||||||||||
| df1(t)/dt = C1 f1(t) + C2 f2(t) | I-69 | ||||||||||||
| où C1 et C2 sont des constantes. On peut alors écrire en utilisant les règles de correspondance entre fonctions f(t) et transformées de Laplace F(s) | |||||||||||||
| sF1 – q1(0) = C1 F1 + C2 F2 | I-70 | ||||||||||||
| Un cas particulier est celui de f(t) = K, une constante : | |||||||||||||
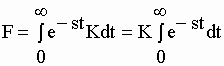 |
I-71 | ||||||||||||
| Pour t = infini, | |||||||||||||
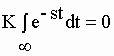 soit K(0/-s) ; |
|||||||||||||
| pour t = 0, | |||||||||||||
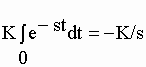 soit K(1/-s). |
|||||||||||||
| Donc | |||||||||||||
| F = K / s | I-72 | ||||||||||||
| qui
est la transformée de Laplace de la constante K. Prenons un autre exemple : |
|||||||||||||
| f(t) = Ae-at | I-73 | ||||||||||||
| La transformée de Laplace de cette fonction s’écrit | |||||||||||||
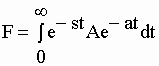 |
I-74 | ||||||||||||
| qui se simplifie en | |||||||||||||
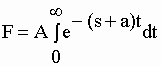 |
|||||||||||||
| Après
intégration, puisque e-(s+a)t
est nul à t = |
|||||||||||||
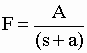 |
I-75 | ||||||||||||
| Animation (Transformée de Laplace d'une bi-exponentielle) | |||||||||||||
| Dressons un tableau de quelques transformées de Laplace : | |||||||||||||
Tableau I-3 : Correspondances entre des fonctions f(t) et leurs transformées de Laplace. |
|
||||||||||||
| Pour illustrer le principe de linéarité de la transformée de Laplace transformons la 4ème fonction du tableau I-3 : | |||||||||||||
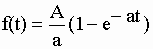 |
I-76 | ||||||||||||
| dont la transformée | |||||||||||||
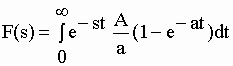 |
I-77 | ||||||||||||
| peut s’écrire, en décomposant f(t) en une fonction f1(t) = A/a et une fonction f2(t) = (-A/a) e-at : | |||||||||||||
| : | |||||||||||||
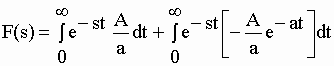 |
|||||||||||||
| En intégrant successivement : | |||||||||||||
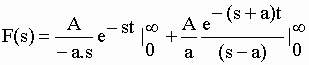
|
|||||||||||||
| ce qui donne bien la formule 4 du tableau I-3 : | |||||||||||||
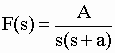 |
I-78 | ||||||||||||
| L’étape suivante consiste à retrouver la fonction f(t) à partir de sa transformée de Laplace F(s). Pour cela on utilise un tableau d'équivalences comme le tableau I-3, mais on peut ne pas y trouver les formules adéquates, ou bien on établit soi-même le réseau d’équations à partir des transformées de Laplace et l’on obtient exactement toutes les formules désirées. Dans ce cas on utilise la méthode des résidus (intégrale de Mellin-Fourier) où la fonction f(t) est la somme algébrique des résidus | |||||||||||||
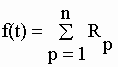 |
I-79 | ||||||||||||
| Les résidus Rp sont calculés à partir des pôles "sp" des transformées de Laplace. Un pôle sp (point de singularité de la fonction) est une valeur de "s" telle que la fonction F(s) est indéterminée. Le résidu Rp est alors : | |||||||||||||
| Rp = (s-sp).F(s).e+st | I-80 | ||||||||||||
| Par exemple la fonction F(s) n° 4 du tableau I-3 "F(s) = A /[s (s + a)]" a deux pôles s1 = -a et s2 = 0 pour lesquels le dénominateur du rapport est nul et rend la fonction indéterminée. Utilisons cette propriété pour retrouver f(t) n°4 du tableau I-3 : | |||||||||||||
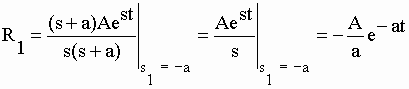 |
I-81 | ||||||||||||
| où l'on a bien pris soin d'éliminer (s+a) du numérateur et du dénominateur, avant de remplacer s par –a. | |||||||||||||
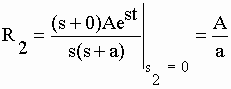 |
I-82 | ||||||||||||
| où (s+0) au numérateur et s au dénominateur sont éliminés avant de remplacer s par 0 pour obtenir le résultat "A / a". Puisque f(t) est égal à la somme des résidus (R1+R2) : | |||||||||||||
|
I-83 | ||||||||||||
| qui est bien la fonction recherchée du tableau I-3. | |||||||||||||
| Animation (Transformation inverse de Laplace pour une bi-exponentielle) | |||||||||||||