Chapitre I Eléments de mathématiques, calcul matriciel, transformations de Laplace |
|||
| III. Calcul matriciel (suite et fin) | |||
| Comment
calcule-t-on un déterminant ? Seules les matrices carrées peuvent se résoudre à un déterminant. Suivant la taille de la matrice, nous utiliserons deux techniques. + pour les matrices d’ordre 2 ou 3 telle que : |
|||
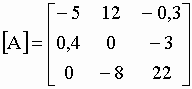 |
I-42 | ||
| on peut utiliser la méthode que nous désignerons par méthode directe. La valeur du déterminant |A| est obtenue par la somme des produits en diagonale dans le sens positif (de gauche à droite en partant du haut) et dans le sens négatif (de droite à gauche en partant du haut) de la manière suivante : | |||
| |A| = + (-5*0*22) +
(12*-3*0) +(-0,3*0,4*-8) sens positif, - (-0,3*0*0) – (12*0,4*22) – (-5*-3*-8) sens négatif = + 0 + 0 + 0,96 – 0 – 105,6 +22 = 15,36. |
I-43 | ||
|
Animation (Calcul d'un déterminant de matrice 3x3 par la méthode
directe) Exercices (Calcul de déterminants de matrices 3x3) |
|||
| +
pour les matrices carrées d’ordre 4 et plus :
La méthode précédente de calcul du déterminant n’est plus applicable. Nous utiliserons la partition de la matrice en cofacteurs. Le cofacteur Cij de l’élément xij (i désigne le numéro de la ligne et j celui de la colonne) de la matrice [Z] suivante : |
|||
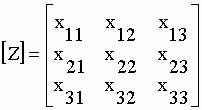 |
I-44 | ||
| est égal à (-1)1+j * |Mij| où |Mij| est le minorant de xij ou la matrice obtenue en supprimant la ième ligne et la jème colonne de la matrice [Z]. Soit par exemple : | |||
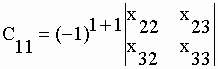 , or (-1)2
= +1 , or (-1)2
= +1
|
I-45 | ||
| En généralisant, (-1)n = +1 et (-1)n+1 = -1, n étant un nombre pair positif. | |||
| Le déterminant de la matrice [Z] (équation I-44) est égal à la somme des produits de chaque cofacteur d’une ligne ou d’une colonne par son élément. Par exemple, en prenant les cofacteurs des éléments de la ligne 1 de [Z] : | |||
| |Z| = x11C11 + x12C12 + x13C13 | I-46 | ||
| ou ceux des éléments de la colonne 2 de [Z] : | |||
| |Z| = x12C12 + x22C22 + x32C32 | I-47 | ||
| etc. | |||
| A partir de ses observations nous pouvons établir une règle pratique des signes des cofacteurs d’une matrice carrée que nous utiliserons souvent : | |||
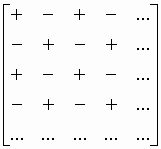 |
I-48 | ||
| Notons
que les cofacteurs des éléments x11, x22,
x33, etc…de la diagonale positive sont
tous positifs. La partition peut s’effectuer sur n’importe quelle matrice carrée ce qui va nous permettre de vérifier les résultats obtenus précédemment (équation I–43). Reprenons notre matrice [A] d’ordre 3 : |
|||
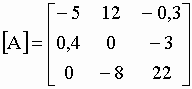 |
I-49 | ||
| dont le déterminant |A| = 15,36. On choisit une ligne ou une colonne. Prenons par exemple la première ligne constituée des éléments –5, 12 et –0.3 : | |||
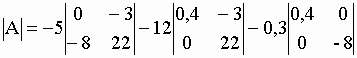 = -5*(-24)–12*(8,8) –0,3*(-3,2) = 15,36 |
I-50 | ||
| Le
déterminant est la somme des cofacteurs d’une ligne
ou d’une colonne quelconque. Essayons avec la première colonne : |
|||
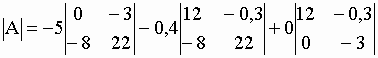 = -5*(-24) –0,4*(261,6) = 15,36 |
I-51 | ||
| puis la deuxième colonne : | |||
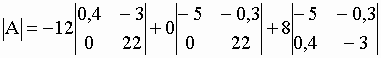 = -12*(8,8) +8*(15,12) = 15,36 |
I-52 | ||
| A
chaque essai, le résultat est identique à celui de
l’équation I-43. Les calculs sont simplifiés
lorsque la ligne ou la colonne comporte des éléments
nuls. Il est donc judicieux de choisir la ligne ou la
colonne de la matrice comportant le plus
d’éléments nuls. Pour des matrices carrées
d’ordre supérieur à 4, il est nécessaire de
résoudre chaque minorant à son sous-minorant pour
qu’il ne dépasse pas l’ordre 3. Animation (Calcul d'un déterminant de matrice 3 x 3 avec partition) Exercices (Calcul de déterminants de matrices 4 x 4) A présent revenons à notre équation matricielle I-35 à trois inconnues qui est du type de celles que nous utiliserons pour résoudre les problèmes posés par l’analyse des flux. Pour obtenir les valeurs de x, y et z, deux méthodes seront utilisées, 1) la méthode de Cramer (plus utile pour les systèmes algébriques que pour les systèmes numériques) et 2) le produit de la matrice carrée inversée [A]-1 par [B] puisqu’il n’est pas possible de diviser directement une matrice par une autre. + Avec la méthode de Cramer la matrice [A], modifiée en substituant le vecteur [B] à l’une de ses colonnes, est divisée par son déterminant |A| avant modification. Pour calculer successivement les trois inconnues x, y et z (équations I-53 à 55) on remplace tour à tour par [B] (rouge) les colonnes 1, 2 et 3 dans la matrice [A] du numérateur : |
|||
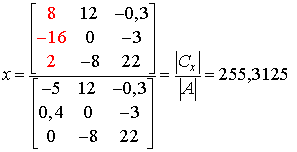 |
I-53 | ||
| où |Cx| = 3921.6 est le déterminant du numérateur et |A| = 15,36 celui du dénominateur. | |||
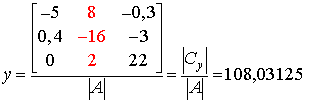 |
I-54 | ||
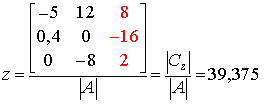 |
I-55 | ||
| Animation (Résolution d'une équation à 3 inconnues par la méthode de Cramer) | |||
| On
peut vérifier que la méthode classique de substitution
donne les mêmes résultats. + Résolution par [A]-1*[B] : l’inversion de matrice est une opération assez délicate et le secours d’un ordinateur est indispensable pour inverser de grosses matrices. Seules les matrices carrées non nulles peuvent s’inverser. Commençons par transposer la matrice [A] en matrice [A]T. La transposition consiste à faire pivoter la matrice autour de la diagonale pour que les lignes deviennent colonnes et les colonnes lignes (I-56). |
|||
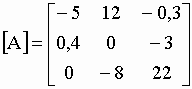
|
I-56 | ||
| On peut vérifier que le déterminant de la transposée est identique à celui de la matrice initiale. Nous devons obtenir une matrice inverse [A]-1 dont le déterminant est égal à 1/15,36 = 0,065104. Pour cela on multiplie la matrice des cofacteurs de la matrice transposée [A]T par l’inverse du déterminant |A|T de la matrice transposée égal à |A| (équations I-43 et I-49 à 52). | |||
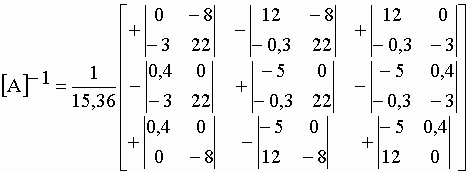 |
I-57 | ||
| En divisant chaque cofacteur par 15,36 on obtient la matrice inversée : | |||
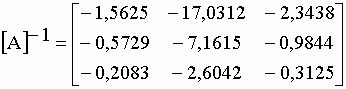 |
I-58 | ||
| dont
on peut vérifier que le déterminant |A|-1
est bien égal à 0,065104. Animation (Inversion de matrice 3 x 3) Exercices (Inversion de matrices 3 x 3) Exercices (Inversion de matrices 4 x 4)
|
|||
| On peut donc calculer le produit [A]-1[B]=[X] : | |||
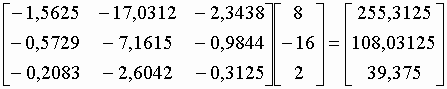 |
I-59 | ||
| qui
nous donne, dans la matrice scalaire résultat [X] et de
haut en bas, les valeurs de x, y et z identiques à
celles calculées par la méthode de Cramer. Exercices (Résolution d'équations à 3 inconnues) Exercices (Résolution d'équations à 4 inconnues) |
|||
| Les matrices présentent d’autres propriétés intéressantes que nous découvrirons lors de leur utilisation dans les chapitres suivants. | |||
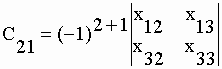 , or (-1)3
= -1
, or (-1)3
= -1

