Chapitre I Eléments de mathématiques, calcul matriciel, transformations de Laplace |
|||
| III. Calcul matriciel | |||
| Considérons le réseau suivant de trois équations à trois inconnues (x, y et z) : | |||
| -5x +12y – 0,3z = 8 0,4x – 3z = -16 -8y + 22z = 2 |
I-33 | ||
| La
méthode classique de résolution de ce système par
substitution est aisée mais devient très lourde avec
l’augmentation du nombre d’inconnues et
d’équations. La résolution par le calcul matriciel
permet de traiter de gros systèmes sans trop de
difficultés. Dans un premier temps on dispose les données en tableaux appelés matrices (lignes, colonnes) pour écrire une équation matricielle du type : |
|||
| [A][X] = [B] | I-34 | ||
| où [A] est la matrice carrée (autant de lignes que de colonnes) des coefficients devant les inconnues, [X] la matrice scalaire ou vecteur des inconnues et [B] la matrice scalaire ou vecteur des résultats. Ce qui nous donne l’équation : | |||
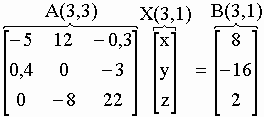 |
I-35 | ||
| Ainsi
l’augmentation du nombre d’inconnues aura pour
effet d’augmenter la taille de la matrice [A] dans
l’équation I-35 et d’allonger vers le bas les
vecteurs [X] et [B]. Les chiffres entre parenthèses
représentent le nombre de lignes et de colonnes de la
matrice. La multiplication est l’opération fondamentale impliquant des matrices. Pour diviser une matrice par une autre, il faut d’abord inverser la matrice dénominateur et multiplier la matrice numérateur par l’inverse de la matrice dénominateur : |
|||
| [A] / [B] = [A][B]-1 | I-36 | ||
| La matrice [A] doit contenir autant de colonnes que la matrice [B] contient de lignes : | |||
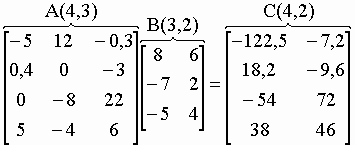 |
I-37 | ||
| La matrice résultats [C] de l’équation I-37 contient autant de lignes que la matrice [A] et autant de colonnes que la matrice [B]. Ces correspondances résultent d’une organisation rigoureuse des données dans le calcul matriciel. Chaque valeur de la matrice [C] est la somme des produits des valeurs d’une ligne de [A] par les valeurs d’une colonne de [B] comme il est détaillé dans l’équation I-38 suivante : | |||
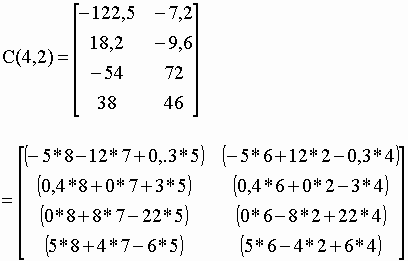 |
I-38 | ||
| Chaque élément d’une matrice est répertorié en fonction de sa position dans la matrice. Il est identifié par deux indices, le premier correspondant à la ligne et le second à la colonne qu’il occupe dans la matrice (I-39) : | |||
 |
I-39 | ||
| Pour bien comprendre la méthode de calcul examinons la valeur 72 de la matrice [C] (équation I-37) à la position c32. Elle est obtenue par la somme des produits d’éléments des matrices [A] et [B] : | |||
| c32 = (a31*b12 + a32*b22 + a33*b32) = (0*6 + -8*2 +22*4) | I-40 | ||
| où les lettres a, b, et c font références respectivement aux matrices [A], [B] et [C] de l’équation I-37. L’élément c21=18,2 de la matrice [C] a été obtenu de la même manière : | |||
| c21 = (a21*b11 + a22*b21 + a23*b31) = (0,4*8 + 0*7 +3*5) | I-41 | ||
| S’il n’est pas possible de diviser une matrice par une autre (équation I-36), on peut la diviser par le déterminant de la matrice au dénominateur.. Le déterminant |Z| d’une matrice [Z] est l'expression de cette matrice réduite à un seul terme ou chiffre si la matrice est numérique. Il s’apparente à une constante. Or pour diviser une matrice par une constante, il suffit de diviser chaque élément de la matrice par cette constante ou de le multiplier par l’inverse de cette constante. | |||

