Chapitre I Eléments de mathématiques, calcul matriciel, transformations de Laplace II. Rappels d’algèbre (suite) |
|||
| d- Exponentielles et logarithmes
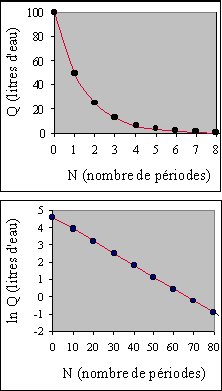
Très souvent le taux de variation d’une grandeur naturelle (physique ou biologique) est proportionnel à cette grandeur. Prenons l’exemple d’un réservoir cylindrique contenant 100 litres d’eau que l’on vidange par un petit robinet situé au plus bas du réservoir. Il faut autant de temps pour vider la moitié du réservoir (50 litres) qu’il n’en faut pour vider la moitié de ce qui reste (25 litres) et pour vider les 12,5 litres de ce qui reste encore, etc… Le temps nécessaire à l’élimination de la moitié du contenu représente la "période" ou encore t1/2 la "demi-vie" de l’eau dans le réservoir. Représentons sur un graphique (Fig. I-2) le volume Q en litres d’eau restant dans le réservoir en fonction du nombre N de périodes écoulées, chaque période ou t1/2 étant de 10 minutes : |
|||
Figure I-2 : Représentation en coordonnées arithmétiques (en haut) et semi-logarithmiques (en bas) du contenu Q d’un réservoir d’eau en cours de vidange en fonction du nombre N de périodes ou demi-vies. L'animation permet de visualiser, dans les deux représentations, les changements des courbes en fonction de la valeur de la constante exponentielle "a". |
|
||
|
La courbe du haut (Fig. I-2) en coordonnées arithmétiques n’est pas rectiligne. Lorsque la variable dépendante Q est remplacée par son logarithme népérien (courbe du bas en coordonnées semi-logarithmiques) on obtient une droite représentative d'une relation linéaire entre "ln Q" et le temps écoulé "t1/2.N" qui peut se traduire par l’équation logarithmique : |
|||
| ln Q = - k.t1/2.N + ln Q(0) | I-23 | ||
| dans laquelle "Q(0)"
représente la quantité d’eau dans le réservoir au début de la vidange (soit 100
litres) et "k" la constante de vidange exprimée en fraction de l’eau du
réservoir éliminée par minute. La pente de la courbe logarithmique est égale à
"- k". La courbe de gauche est traduite par l’équation exponentielle : |
|||
| Q = Q(0).e-k.t½.N | I-24 | ||
| où Q(0) devient "coefficient exponentiel" et k "constante exponentielle". On dit que la vidange du réservoir d’eau suit une loi exponentielle ou logarithmique. En posant le temps t en minutes (=t1/2.N) comme variable indépendante, l’exponentielle ci-dessus est remplacée par : | |||
| Q = Q(0).e-k.t | I-25 | ||
| qu’on simplifie en "1/2=e-k.t½" d’où ln 0,5=-k.t1/2. La constante k=-ln0,5/10=0,069315/minute. |
|||
| Dans la pratique seuls les réels positifs supérieurs à 0 ont un logarithme. L’avantage essentiel des logarithmes est de simplifier les calculs. En effet, de même qu’une exponentielle est remplacée par une expression linéaire, un produit est remplacé par une somme : | |||
| et | ln(A.B) = lnA +
lnB ln(A/B) = lnA - lnB |
I-27 | |
| On peut vérifier que le produit A.e-a.t*B.e-b.t=A.B.e-(a+b).t. En effet : | |||
| ln(A.e-a.t * B.e-b.t) = ln(A.e-a.t) + ln (B.e-b.t) = - (a+b).t + lnA + lnB = – (a+b).t + ln(A.B) |
I-28 | ||
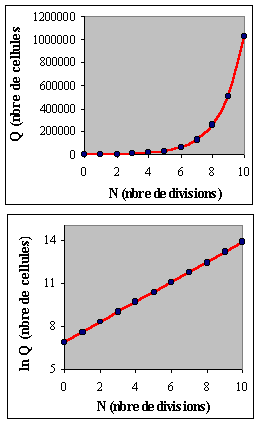
| Parmi les exemples biologiques, la croissance d’une population de cellules dans les premiers temps suivant la mise en culture est de type exponentiel : | |||
| Q = Q(0).e+k.t½.N et ln Q = + k.t1/2.N + ln Q(0) | I-29 | ||
| Q(0) est le nombre initial de cellules et Q le nombre au temps t1/2.N. La population est doublée après chaque période de division. Dans ce cas les courbes exponentielle et logarithmique (Fig. I-3) évoluent positivement : | |||
Figure I-3 : Croissance d’une population cellulaire en coordonnées arithmétiques (haut) et semi-logarithmiques (bas). L'animation permet de visualiser, dans les deux représentations, les changements des courbes en fonction de la valeur de la constante exponentielle "a". |
|
||
| Les équations décrivant le devenir des substances dans les systèmes biologiques sont généralement des sommes d’exponentielles décroissantes dont la structure est relativement simple : | |||
| f(t) = A.e-at + B.e-bt + ... + M.e-mt | I-30 | ||
| "A, B, ..., M"
représentent les coefficients exponentiels, "a, b, ..., n" les constantes
exponentielles. La variable indépendante "t" représente le temps. La simplicité structurelle de la fonction f(t) ne doit pas faire oublier la complexité des paramètres cinétiques cachés dans les coefficients et constantes exponentielles. Nous le découvrirons dans les chapitres à venir. Nous retiendrons pour le moment que dans la fonction pluri-exponentielle I-30 la variable indépendante t est nulle ou positive. Il en découle que la valeur de chaque terme exponentiel, e-at à e-mt, est comprise entre e-0=1 (pour t=0) et e-¥ =0 (pour t=¥ ). Cette fonction est dérivable (voir Tab. I-1) : |
|||
| df(t)/dt = -a.A.e-at - b.B.e-bt - ... - m.M.e-mt | I-31 | ||
| et intégrable (voir Tab. I-2) : | |||
| ò f(t).dt = -(A.e-at)/a+ (B.e-bt)/b+ ... + (M.e-mt)/m + K | I-32 | ||
| Pour t = 0 la dérivée est égale
à – (a.A + b.B + … + m.M). Dans l’intervalle de temps compris entre 0 et ¥ , l’intégrale définie vaut (A/a+B/b+…+M/m). Nous aurons très largement à utiliser ces propriétés lors de l’élaboration et de l’analyse des modèles cinétiques. Par la suite nous utiliserons indifféremment l’un ou l’autre des deux modes de présentation de l’exponentielle : M.e-m.t ou M.exp(-m.t). |
|||