Chapitre I Eléments de mathématiques, calcul matriciel, transformations de Laplace II. Rappels d'algèbre (suite) |
||||||||||||||||||
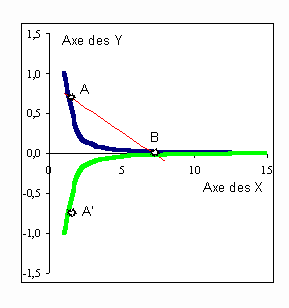
| c- Dérivées et primitives Pour illustrer le concept de dérivée considérons, par exemple, la fonction f(x)=y=1/x. Elle est indéterminée pour x=0 et nulle pour x=±∞ . Sur la figure I-1 sont représentées les courbes de la fonction (bleue) et de sa dérivée (verte) pour x>0. Considérons sur la courbe bleue le point A de valeur y1 pour x1 et le point B de valeur y2 pour x2. La pente de la droite en rouge passant par les points A et B est le rapport des différences Dy/Dx=(y2–y1)/(x2–x1). En remplaçant y1 et y2 respectivement par 1/x1 et 1/x2 : |
||||||||||||||||||
| D y / D x = (1/x2 – 1/x1) / (x2 – x1) = – 1/(x1x2) | I-10 |
|||||||||||||||||
| Lorsque le point B se rapproche du
point A , x2 tend vers x1 et D x
vers 0. Par voie de conséquence le rapport Dy/Dx tend
vers dy1/dx1=–1/x12
qui est la dérivée de la fonction f(x) au point A.
Cette dérivée d'abscisse x1 est
représentée par le point A' de la courbe verte (Fig.
I-1) dont chaque point est la dérivée d'un point de
même abscisse de la courbe bleue. Par extension, la fonction f(x) ou y a pour fonction dérivée df(x)/dx ou dy/dx=–1/x2. |
||||||||||||||||||
Figure I-1 : Expression graphique d’une fonction y = 1/x (courbe bleue) et de sa dérivée dy/dx = -1/x² (courbe verte). |
|
|||||||||||||||||
| Le tableau I-1 présente quelques fonctions f(x) associées à leurs dérivées f(x)/dx parmi celles que nous utiliserons le plus souvent : | ||||||||||||||||||
Tableau I-1 : Dérivées f(x)/dx de fonctions primitives f(x). |
|
|||||||||||||||||
| où x représente la variable
indépendante ; a, n et m sont des constantes ;
ln signifie "logarithme népérien ou naturel"
de la variable ou de la constante qui suit. A titre
d’exemple la fonction f(x)=x–12
a pour dérivée f(x)/dx=–12.x–13.
Notons que la dérivée d’une constante est nulle.
Ainsi pour la fonction f(x)=x–12+7 la
dérivée f(x)/dx est aussi égale à –12.x–13. Les propriétés des fonctions sont telles que la dérivée d’une somme de fonctions est la somme des dérivées de chacune des fonctions. On l’exprime habituellement par |
||||||||||||||||||
| d(u + v) = du + dv d(u.v) = v.du + u.dv d(u/v) = (v.du + u.dv) / v2 |
I-11 I-12 I-13 |
|||||||||||||||||
| Par ailleurs le produit d’une constante "a" par une fonction "u" a pour dérivée le produit de la constante par la dérivée de la fonction : | ||||||||||||||||||
| d(a.u) = a.du | I-14 |
|||||||||||||||||
|
L'intégration permet de retrouver une fonction primitive à partir de sa dérivée. Cette technique sera fréquemment utilisée lors de l'élaboration des modèles mathématiques des systèmes. Ici la relation entre une fonction et sa dérivée peut s'exprimer d'une manière générale par |
||||||||||||||||||
| òf(x).dx = P(x) + K | I-15 |
|||||||||||||||||
|
Il s’agit d’une intégrale non définie où "P(x)" désigne la primitive de la fonction f(x). La constante K, dite constante d’intégration, peut prendre n’importe quelle valeur puisqu’elle est la primitive de f(x) = 0. On peut d'ores et déjà établir le tableau I-2 des principales primitives utilisées par la suite dans le cours : |
||||||||||||||||||
Tableau I-2 : Primitives P(x) de fonctions f(x). |
|
|||||||||||||||||
| où nous retrouvons les
expressions inversées du tableau I-1 des dérivées. Les intégrales sont définies pour un intervalle de la variable x compris entre a et b |
||||||||||||||||||
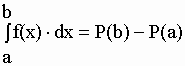 |
I-16 |
|||||||||||||||||
| où P(a) et P(b) sont les primitives de la
fonction pour les valeurs a et b de la variable indépendante x. La
constante K disparaît puisque pour x = a la primitive de f(x) est P(a) +
K et pour x = b elle vaut P(b) + K. Dans les chapitres suivants, nous
aurons à intégrer entre deux valeurs de la variable indépendante t
(temps) comprise généralement entre 0 et ∞ unités de temps (seconde,
minute, heure, …). Illustrons notre propos à partir d’une fonction f(x) simple : |
||||||||||||||||||
| f(x) = –12x + 7 | I-17 |
|||||||||||||||||
| que nous allons intégrer entre deux valeurs de x, a = 2 et b = 9. Dans un premier temps estimons l’intégrale indéfinie | ||||||||||||||||||
| ò(–12x + 7)dx = P(x) + K | I-18 |
|||||||||||||||||
| en appliquant le principe que "l’intégrale de la somme de plusieurs fonctions de x est la somme des intégrales de chacune de ces fonctions". On pose alors comme dérivées du = -12.x qui est le premier terme de notre fonction à intégrer et dv = 7 qui en est le second. Les primitives respectives sont u = –12x(1+1) /(1+1) ou –6x2 et v = 7x(0+1)/(0+1) ou 7x. La somme des primitives P(x)+K est égale à – 6x2+7x+K. Pour obtenir l’intégrale définie | ||||||||||||||||||
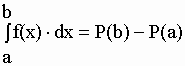 |
I-19 |
|||||||||||||||||
| on remplace x par sa valeur a pour
avoir P(a)=–10+K et par sa valeur b pour avoir
P(b)=–423+K. La différence
P(b)–P(a)=–413. Exercice : intégrer la fonction f(x)=–3x3+5x2–1 pour les valeurs de x comprises entre a=–2 et b=+2. Réponse : P(x)=–3/4 x4 + 5/3 x3 – x + K ; P(a)=–70/3 + K ; P(b)=–2/3 + K ; P(b)–P(a)=68/3. |
||||||||||||||||||
| Dans les prochains chapitres nous aurons l’occasion d’intégrer des sommes de fonctions comme nous venons de le faire ainsi que des produits de fonctions. Nous avons établi plus haut la formule I-12 qui exprime la dérivée d’un produit "u.v" de deux fonctions. L’intégration procède à l’inverse de la dérivation, ce qui nous permet d’exprimer l’intégration "par parties" avec les formules | ||||||||||||||||||
| uv
= òudv +
òvdu òudv = uv – òvdu |
I-20 |
|||||||||||||||||
| Intégrons par exemple la fonction f(x)=(– 2x+7)(3x2–2). On pose u=–12x+7 et dv=3x2–2, de sorte que du=–12 et v=x3–2x. Il vient | ||||||||||||||||||
| òudv = (– 12x
+ 7)( x3
– 2x) + 12ò(x3
– 2x)dx = – 9x4 + 7x3 + 12x2 – 14x + K |
I-21 |
|||||||||||||||||
| Vérifions ce résultat en intégrant la fonction équivalente f(x)=–36x3+21x2+24x–14 qui n’est autre que le produit (–2x+7)(3x2–2) : | ||||||||||||||||||
| òf(x)dt = –
36òx3dx
+ 21òx2dx
+ 24òxdx – 14x = – 9x4 + 7x3 + 12x2 – 14x + K |
I-22 |
|||||||||||||||||
| On obtient bien le même
résultat. Exercice : intégrons la fonction f(x)=xAe–B.x dans l’intervalle de x compris entre 0 et l’infini. Réponse : admettons que la fonction f(x) est le produit de deux fonctions f1(x)=Ax et f2(x)=e–Bx. Dans ce cas nous appliquons la technique de l’intégration par parties en choisissant u=A.x et dv=e–Bx qui font que du=A et v=–(e–Bx)/B (voir tableaux I-1 et 2). L’intégrale indéfinie : |
||||||||||||||||||
| òudv = –
(A/B)xe-Bx + (A/B)òe-Bx dx = – (A/B)xe-Bx – (A/B)e-Bx/B + K = – (A/B2)e-Bx(1+Bx). |
||||||||||||||||||
| Pour x=0, f(x)=–A/B2 ; pour x=∞, f(x)=0. L’intégrale définie pour 0≤x≤∞ est donc égale à A/B2. | ||||||||||||||||||