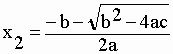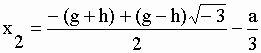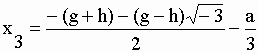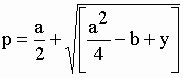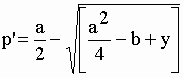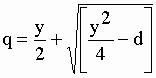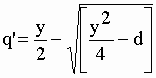Chapitre I Eléments de mathématiques, calcul matriciel, transformations de Laplace II. Rappels d’algèbre a- Identités remarquables Il est indispensable de se remémorer les identités remarquables que nous utiliserons le plus souvent : |
|||||
| (a + b)2
= a2 + 2ab + b2 (a – b)2 = a2 – 2ab + b2 |
I-1 |
||||
| a2
–
b2 = (a + b)(a
– b) a2 + b2 = (a + bi)(a – bi) |
I-2 |
||||
| où i = Ö–1 et donc i2
= –1. b- Equations des second, troisième et quatrième degrés à une inconnue Les constantes exponentielles ou macroconstantes a, b,.... , m des équations qui décrivent les systèmes à un instant t donné sont les racines réelles d’équations de degré 1, 2, …, n suivant que le système est constitué de 1, 2, …, n compartiments.. L’équation générale du second degré : |
|||||
| ax2 + bx + c = 0 | I-3 |
||||
| a 2 racines : | |||||
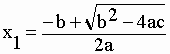
|
I-4 |
||||
| Exercices :
trouver les racines des équations suivantes. –3x2 +5x –2 = 0 rép. : x1 = 0,66666…. ; x2 = 1 x2 +12x = 0 rép. : x1 = 0 ; x2 = -12 Accéder aux exercices numériques (Equations du second degré) L’équation générale du 3ème degré |
|||||
| x3 + ax2 + bx + c = 0 | I-5 |
||||
| a trois racines que l’on obtient en calculant successivement : | |||||
| d = (3b
─ a2) / 9 e = (2a3 ─ 9ab + 27c) / 54 |
|||||
| Si x est un nombre imaginaire les racines x1, x2 et x3 sont réelles et inégales. On les obtient à partir de | |||||
|
I-6 |
||||
| Les 3 racines sont inégales et réelles si d<0 et –1< cosj <1, sinon x1 est réel et les deux autres sont des nombres complexes. Il faut alors procéder autrement en calculant successivement : | |||||
|
|||||
| puis les racines elles-mêmes : | |||||
|
I-7 |
||||
|
Exercices :
trouver les racines des équations suivantes : 1) x3+11x2 +26x + 16 = 0 réponse : d = (3*26-112)/9 = – 4,777777...... ; e = (2*113-9*11*26+27*16)/54 = 9,6296296. Calculons cos φ = 0,9220844..... Puisque d < 0 et cos φ compris entre –1 et +1, il y a 3 racines réelles inégales : x1 = –8 ; x2 = –1 ; x3 = –2. 2) x3 + 0,12x2 + 0,0041x + 0,000025 = 0 réponse : d = –2,3333....10-4 ; e = –0,0000055 ; cos φ = –1,54311... <–1 indique des racines complexes. En appliquant les formules pour un tel cas les racines sont : x1 = –7,736...10-3 ; x2 = -0,05613...+ i.0,008936... ; x3 = –0,05613...- i.0,008936... Notons que x1 est réel et que x2 et x3 sont des racines complexes dites conjuguées car leurs éléments sont identiques mais avec changement de signe pour le second tel que m+i·n et m–i·n. Accéder aux exercices numériques (Equations du 3ème degré) L’équation générale du 4ème degré : |
|||||
| x4 + ax3 + bx2 + cx + d = 0 | I-8 |
||||
| a quatre racines x1, x2, x3 et x4. On les obtient à la suite de plusieurs étapes dont la première consiste à extraire la racine réelle y de plus grande valeur de l’équation du 3ème degré | |||||
| y3 + ry2 + sy + t = 0 | |||||
| où r = –b, s = ac – 4d et t = d(4b – a2) – c2. On pose ensuite | |||||
|
et |
|
|||
|
et |
|
|||
| Les racines de l’équation du 4ème degré sont les racines des trinômes : | |||||
x2 + px + q = 0 |
et |
x2 + p'x + q' = 0 |
I-9 |
||
| Exercice : trouver les quatre racines de l’équation suivante : x4 + 5,67.x3 + 11,13.x2 + 8,557.x + 1,866 = 0 réponse : on obtient les racines intermédiaires y1 = 3,148056 ; y2 = 4,026673 et y3 = 3,955271. On retient la racine y2 pour calculer les quatre racines, x1 = –1,553899 ; x2 = –2,247485 ; x3 = –1,516221 et x4 = –0,352395. Accéder aux exercices numériques (Equations du 4ème degré) |
|||||