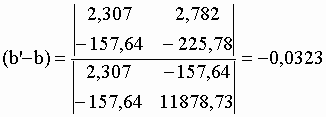Chapitre VI Ajustement des courbes aux données expérimentales. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Jusqu’à présent nous avons
utilisé des données idéalisées du métabolisme de
l’eau, des hormones thyroïdiennes, du diazepam.
Elles étaient calculées par ordinateur à partir de
paramètres dont les valeurs étaient préétablies et
devaient être retrouvées après élaboration des
modèles choisis. Elles avaient une fonction
essentiellement pédagogique vis-à-vis du contrôle de
la maîtrise de l’analyse compartimentale. Dans la
réalité, les résultats sont entachés d'incertitudes
ou erreurs d'origines diverses liées à l'imprécision
des mesures, à la variabilité physiologique du
matériel vivant, au moment de l'expérience, etc …
Les points expérimentaux se répartissent de part et
d'autre d'une courbe dont il faut retrouver le tracé le
plus probable statistiquement par des méthodes
mathématiques "d'ajustement des courbes aux
données expérimentales". Les données du tableau VI-1 illustrent un cas où l'on a mesuré le pourcentage d'une substance S éliminée dans les urines en fonction des heures qui suivent son injection par voie intraveineuse. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Tableau VI-1 : Quantités cumulées d'une substance S dans les urines en fonction des heures suivant son injection par IV. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
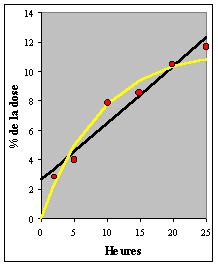
| Les valeurs sont reportées sur un graphique (Fig. VI-1). A première vue les points expérimentaux apparaissent à peu près alignés de part et d'autre d'une droite qui pourrait être du type "y = ax + b". | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Figure VI-1 : Quantités cumulées (points rouges) d'une substance S dans les urines après son injection par IV. Les courbes sont ajustées par "régression linéaire" (droite noire) et "régression non linéaire" (courbe jaune). |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Dans ce cas, l'ajustement de la droite à l'ensemble des points expérimentaux est obtenu par "régression linéaire" qui minimise la somme des carrés des écarts entre les points expérimentaux de coordonnées y et leurs valeurs correspondantes y' sur la droite théorique. Celle-ci a pour pente : | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
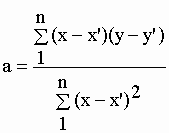 |
VI-1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Les valeurs théoriques de la pente a et de l'ordonnée à l'origine b sont calculées au mieux comme : | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
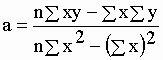 = 0,3866 fraction de la dose /
heure = 0,3866 fraction de la dose /
heure
|
VI-2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| où n représente le nombre de
points expérimentaux et x et y leurs coordonnées
(heures et % de la dose). D'un point de vue physiologique, l'ajustement par "régression linéaire" n'est pas satisfaisant. D'une part parce qu'il ne peut y avoir de substance S dans les urines au temps t= 0 après l'injection. Le point à 0 heure vaut donc 0 % de la dose (et non 2,6385). D'autre part parce que la régression linéaire implique une augmentation constante de la quantité de substance S dans les urines, alors qu'elle ne peut dépasser une valeur correspondant à la fraction éliminée par voie urinaire. Dans ces conditions il est raisonnable d'ajuster à une courbe de type exponentiel |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| y = a (1– eb x) | VI-3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| avec b pour asymptote. Un tel
ajustement est obtenu par "régression non
linéaire" à l'aide d'une des méthodes utilisant
le principe des "moindres carrés". En quoi consiste la régression non linéaire par la méthode des "moindres carrés" ? Comme pour la régression linéaire il s'agit de minimiser la "somme des carrés des écarts" SCE = S (y'-y)² entre les valeurs initiales y et leurs valeurs correspondantes y' sur la courbe théorique. Il est nécessaire de connaître l’équation présumée de la courbe à analyser dont on estime grossièrement, dans un premier temps, les paramètres. Prenons par exemple dans l’équation VI-3 "a = 12 % de la dose" et "b = – 0,08 / h". Les valeurs y' de la courbe calculées à partir de ces paramètres sont mises en regard des valeurs y expérimentales (Tab.VI-2, col. 2 et 3 ) et représentées par la courbe rouge (Fig. VI-2). Tous les points expérimentaux apparaissent au-dessus de la courbe calculée. Pour que les points soient mieux répartis de part et d'autre de la courbe il faut modifier les paramètres. La méthode d'ajustement par les moindres carrés (Deming, 1943; Nogami et al., 1969) amène par itérations successives la SCE au minimum possible en partant de la relation matricielle : |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
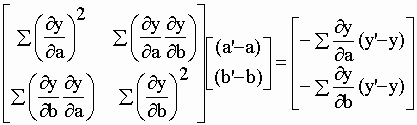 |
VI-4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| dans laquelle les dérivées de la fonction y (Eq. VI-2) par rapport aux variables momentanées a et b sont respectivement : | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ¶ y/¶ a = 1 – exp (b x) et ¶ y/¶ b = – x a exp (b x) | VI-5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Tableau VI-2 : Détail des éléments numériques nécessaires à la détermination des paramètres de l'équation VI-3 par régression non linéaire des moindres carrés pour les paramètres initiaux a = – 0,08 et b = 12.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Le tableau VI-2 rassemble les éléments de la matrice carrée calculés avec les valeurs obtenues à partir des estimations visuelles de a et b. Il est commode d'utiliser la règle de Cramer (voir chap. I) pour le calcul des écarts entre les paramètres a et b d'une estimation à la précédente (Eq. VI-6). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
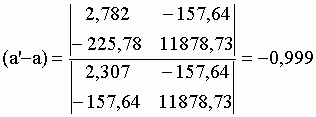
|
VI-6 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Après la 3ème itération, les différences (a' - a) et (b' - b) sont quasiment nulles et la somme des carrés des écarts SCE est à peu près stabilisée (Tab. VI-3). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Tableau VI-3 : Valeurs de la quantité de substance S accumulée dans les urines (% de la dose) en fonction du temps (heures après injection) obtenues après 3 itérations (y' (it.1-3)) en regard des valeurs expérimentales (y exp). Les paramètres a et b de la 3ème colonne sont estimés visuellement. SCE = Somme des carrés des écarts.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
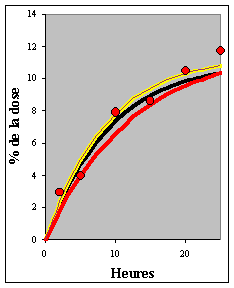
| La figure VI-2 visualise les quatre courbes établies avec les valeurs du tableau VI-3. L'expression numérique de la courbe la mieux ajustée aux valeurs expérimentales est donc | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| y = 11,516 (1 – e–0,113 x) | VI-7 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Les méthodes d'ajustement par régression non linéaire font encore souvent référence au principe des moindres carrés mais les techniques informatiques de calcul de plus en plus performantes et sophistiquées ont permis le développement de variantes favorisant la sécurité dans les calculs, telle que la convergence rapide vers les paramètres optimaux. Des "facteurs de pondération" désignés par w sont souvent introduits dans la formulation pour réduire le poids des valeurs élevées face aux valeurs faibles. Un facteur w peut être la réciproque de la valeur y expérimentale, ou de son carré y² , ou encore de (y' + y)², etc… | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Figure VI-2 : Courbes établies avec les valeurs du tableau VI-1 à partir des paramètres a et b estimés visuellement (courbe rouge) et après trois itérations successives (courbes noire, mauve et jaune). La courbe jaune est la mieux ajustée aux valeurs expérimentales |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| L'équation matricielle VI-4 est modifiée en conséquence | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
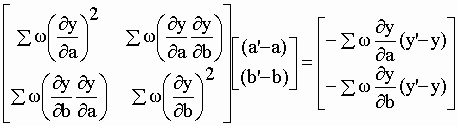 |
VI-8 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| De tels changements conduisent à des différences souvent minimes, parfois non négligeables, de la valeur des paramètres ajustés. Dans notre exemple, après introduction d'un facteur de pondération, les équations des courbes les mieux ajustées sont : | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| y = 11,382 (1 – e–0,117
x) pour w = 1/y y = 11,225 (1 – e–0,122 x) pour w = 1/y² y = 11,234 (1 – e–0,122 x) pour w = 1/(y'-y)². |
VI-9 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Elles présentent de légères
différences entre elles et avec l'équation VI-6. Nous ne discuterons pas des qualités des différentes techniques d'ajustement des courbes non linéaires, ce qui est hors de propos ici. Retenons qu'elles sont nombreuses à utiliser le principe des moindres carrés et souvent affublées de noms aussi évocateurs que les désignations de spécialités pharmaceutiques : SIMPLEX, NONMEM, MULTIFIT, FRIGGA, ALIENOR, etc… Au laboratoire, nous avons utilisé avec satisfaction MKMODEL (Holford, 1986). La quasi totalité des calculs du présent ouvrage a été effectuée sur micro-ordinateur à l'aide du tableur Excel 97 de la suite logicielle Microsoft Office 97. D'autres tableurs tels que Lotus 123, Quattro Pro conviennent aussi. Les logiciels mathématiques MathCad et Derive ont été utilisés en particulier comme aide au calcul symbolique, ils permettent en outre l’ajustement non linéaire de courbes. Une calculette avec fonctions mathématiques et statistiques est aussi très utile. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
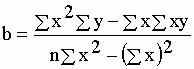 = 2,6385 % de
la dose
= 2,6385 % de
la dose